The Fourier Transform and its Application in Machine Learning
Preface
The Fourier Transform holds significant importance across scientific and engineering domains, serving diverse applications from signal processing to quantum mechanics.

Its relevance has notably expanded into Machine Learning in recent times. This piece delves into the core principles of the Fourier Transform and its increasingly crucial role within Machine Learning applications.
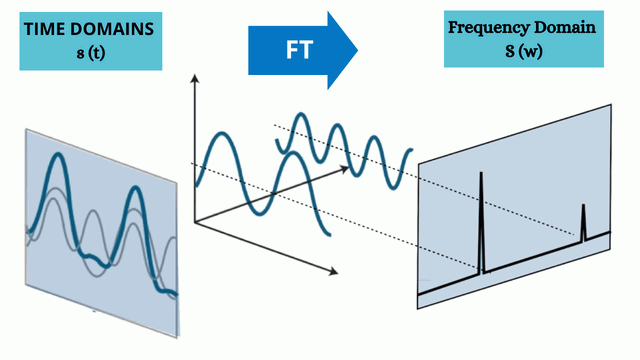
“The Fourier Transform unifies data domains and unveils hidden patterns that reverberate throughout Machine Learning environments..”
Named after the French mathematician and physicist Jean-Baptiste Joseph Fourier, the Fourier Transform is a mathematical procedure that dissects a signal into its component frequencies.
It enables the examination of a signal’s frequency makeup and portrays it within the frequency domain. This transformation proves especially valuable for intricate signals, streamlining the comprehension of their fundamental structures.
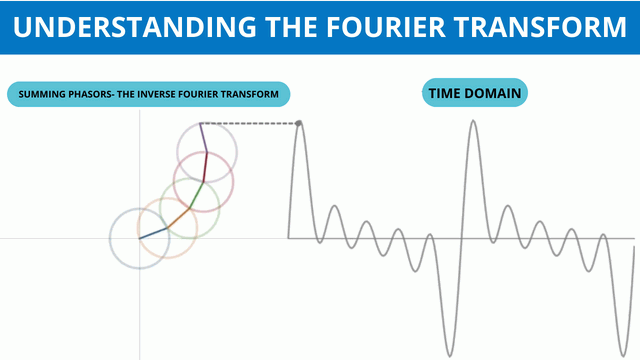
Two prevalent variants of the Fourier Transform include the Continuous Fourier Transform (CFT) and the Discrete Fourier Transform (DFT).
The CFT caters to continuous signals, whereas the DFT is tailored for discrete signals, rendering it especially pertinent to digital data and machine learning endeavors.
The Fast Fourier Transform (FFT) serves as an expedited algorithm for computing the DFT, thereby enhancing its extensive adoption across diverse applications.
Signal processing stands as one of the conventional and firmly established arenas for the Fourier Transform. Its applications span tasks like audio processing, image analysis, and data compression.
For instance, in audio processing, the Fourier Transform aids in identifying diverse frequencies within an audio signal, facilitating activities such as speech recognition, music classification, and noise mitigation.
Within image analysis, the Fourier Transform proves instrumental in extracting texture and pattern details from images. The conversion of images into the frequency domain simplifies the identification of edges, shapes, and other visual attributes.
Such capabilities are vital for tasks including image recognition, object detection, and image compression.
The Fourier Transform’s integration into Machine Learning, a realm centered on creating algorithms that learn from data, has broadened significantly. Its applications within this sphere are varied and influential:
- Time Series Analysis: Abundant in domains like finance, healthcare, and weather forecasting, time series data reigns supreme. Leveraging the Fourier Transform aids in extracting pertinent features from this data by scrutinizing its frequency elements.
This proves pivotal for tasks such as anomaly detection, trend analysis, and forecasting.
- Natural Language Processing: Textual data, when structured as word sequences, parallels a discrete signal. Employing the Fourier Transform enables the analysis of textual content within the frequency domain.
This approach finds applications in text classification, sentiment analysis, and topic modeling.
- Feature Engineering: An integral phase within the machine learning workflow, feature engineering holds immense significance.
Translating data into the frequency domain facilitates the extraction of valuable features that might pose challenges in the time domain. This practice often leads to more resilient and precise machine learning models.
- Convolutional Neural Networks (CNNs): Renowned within the realm of deep learning for image analysis, CNNs offer a popular architectural choice.
Leveraging the Fourier Transform enables the design of convolutional filters specialized in detecting specific frequency elements within images. This enhancement notably bolsters CNN performance in tasks like image classification and object recognition.
- Data Augmentation: A technique employed to amplify the training dataset, data augmentation holds significance. In image processing, the Fourier Transform serves to create augmented data by manipulating the frequency components within images.
This practice significantly enhances the generalization and resilience of machine learning models.
To execute a Fourier Transform for Time Series Analysis in Python, you’ll utilize the numpy and matplotlib libraries. Below is a Python code snippet demonstrating this process with a sample dataset and generating pertinent plots.
If you haven’t installed the required libraries yet, use the following commands:
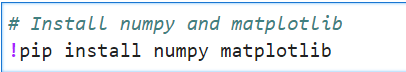
Once installed, here’s an example Python code:

- Two sinusoidal components are created in a sample time series dataset that we create. Replace this with your specific time series data.
- Using np.fft.fft, we execute the Fourier Transform on the time series data.
- Corresponding frequencies are computed utilizing np.fft.fftfreq.
- Two subplots are created: one showcasing the original time series and the other displaying the magnitude of the Fourier Transform.
- Finally, the plots are showcased using plt.show(). Adjust the parameters and data to suit your analysis requirements.

Ensure to substitute the placeholder dataset with your unique time series data when handling real-world information. The provided code generates plots for both the original time series and the Fourier Transform magnitude. Customize the plotting parameters and labels as per your particular requirements.
Conclusion
Last but not least, the Fourier Transform, initially rooted in signal processing, has seamlessly integrated into the core of Machine Learning.
Its capacity to scrutinize and extract frequency details from data holds immense value across multiple ML applications, encompassing time series analysis, natural language processing, feature engineering, and the refinement of deep learning models.
As Machine Learning progresses and broadens its scope, the Fourier Transform stands as a robust tool, empowering researchers and practitioners to unveil profound insights and forge more potent algorithms.
Its versatility and adaptability cement its status as an indispensable element within the modern machine learning arsenal.
FAQs
The Fourier Transform plays a pivotal role in Machine Learning by extracting frequency information from data, aiding tasks like time series analysis, natural language processing, and enhancing deep learning models.
In signal processing, it identifies diverse frequencies within signals, enabling applications such as speech recognition and image compression. In image analysis, it extracts texture and shape details crucial for image recognition and object detection.
Its applications encompass time series analysis for anomaly detection and forecasting, text analysis in NLP for sentiment analysis, and feature engineering to enhance model precision.
Leveraging the Fourier Transform aids in designing specialized convolutional filters within CNNs, boosting their performance in tasks like image classification and object recognition.
Through libraries like numpy and matplotlib, the Fourier Transform can be executed in Python. The provided code snippet demonstrates its application in time series analysis, allowing users to visualize data and its frequency components.
Get access all prompts: https://bitly.com/machine-learning







